Understanding how different functions behave as input values grow is fundamental in computer science, especially in analyzing algorithm efficiency. This tutorial walks you through how to compare functions, understand their rates of growth, and use Big-O notation to describe their behavior concisely.
1. Comparing Simple Functions
Let’s begin by considering two simple functions:
- f(n)=n
- g(n)=n2
We want to observe how their values change as nnn increases.
Step-by-Step Observation
Case 1: f(n)=n
- f(100)=100
- f(101)=101
- f(102)=102
- f(103)=103
We can see that for every increase in n by 1, the output also increases by 1. The function grows linearly.
Case 2: g(n)=n2
- g(100)=10,000
- g(101)=10,201
- g(102)=10,404
- g(103)=10,609
Here, each increment in n results in a larger jump in output. For example:
- From g(100) to g(101): Increase = 201
- From g(101) to g(102): Increase = 203
This tells us that g(n)=n2 grows faster than f(n)=n.
Conclusion
Different functions grow at different rates. As n→∞n, the values of g(n)=n2 grow significantly faster than f(n)=n.
2. Comparing Function Orders: Constants vs Growth
Let’s now consider two more functions:
- t1(n)=2n2
- t2(n)=99n
At first glance, t2(n) may seem larger for small values of n, especially because 99 is a large constant.
Compare at n=50:
- t1(50)=2×502=5000
- t2(50)=99×50=4950
Very close! But now try with a much larger constant in t2(n):
- t2(n)=1,000,000n
Still, as n→∞, t1(n)=2n2 will eventually surpass any linear function due to its higher order of growth.
Key Insight
- Constants affect performance for small nnn.
- For large nnn, the order (or degree) of the function dominates.
- That’s why in asymptotic analysis, we often ignore constants.
3. Understanding Function Orders
Function order refers to how fast a function grows relative to its input. Here’s a table of common function orders, sorted from fastest to slowest growth as n→∞:
| Order | Example |
| n! | Factorial |
| Exponential | |
| Polynomial | |
| n log n | Quasilinear |
| n | Linear |
| Root | |
| log n | Logarithmic |
| 1 | Constant |
You can visually compare these with graphing tools. For example:
- At n=10, n!=3,628,800, while n2=100
- Growth differs drastically as n increases
4. Leading Term and Dominance
Consider a complex function:
![]()
Here, each term grows differently:
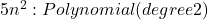
- 1,000,000n: Linear
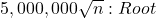
When n=1,000,000,000, the term 5n2 dominates, even though the other terms have huge constants.
This gives us an important rule:
The term with the highest order (fastest growth rate) is called the leading term. It determines the asymptotic behavior of the function.
5. Identifying Leading Terms Using the Order Table
Let’s practice identifying leading terms.
Given:
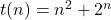 → Leading term: 2n
→ Leading term: 2n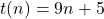 → Leading term: 9n
→ Leading term: 9n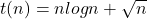 → Leading term: n log n
→ Leading term: n log n → Leading term: 6n3
→ Leading term: 6n3
Always choose the term with the highest order from the table.
6. Comparing Functions by Leading Terms
Once we find the leading terms, we can compare functions more easily.
Case A: Different Orders
Compare:
Here, t1 grows faster because quadratic functions grow faster than linear ones.
Case B: Same Order
Compare:
Both are linear, but t1n grows slower due to its smaller constant.
7. Summary: How to compare functions as n→∞
- Find the leading term of each function.
- Determine the order of each leading term using the order table.
- Compare the orders:
- If orders differ → the function with lower order grows slower.
- If orders are same → compare constants.
- Ignore lower-order terms and constants for large nnn analysis.
8. Introducing Big-O Notation
We now formalize the idea of function growth using Big-O notation.
What is Big-O?
Big-O describes the upper bound of a function’s growth.
Example:
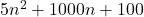
- We write:
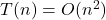
This means that asymptotically, the function grows like n2, and we ignore constants and lower-order terms.
More Examples:
| Function | Big-O Notation |
Big-O helps compare algorithms by their worst-case time complexity.
