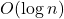Advanced Complexity Evaluation: Addition, Multiplication, Logarithms, and Strings

In this tutorial, we’ll dive deeper into algorithm complexity, focusing on common operations such as addition, multiplication, logarithmic algorithms, and the role of string manipulation in evaluating time complexity.

1. Complexity of Addition and Multiplication

Let’s start by analyzing sequential and nested loops.

Example: Sequential Loops

Suppose we have the following scenario:

One loop iterates over array A of length
Another loop iterates over array B of length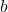

These loops run sequentially, not nested. So we simply add their individual complexities:

$T(a, b) = a + b$

In Big-O notation:

$T(a, b) = O(a + b)$

Example: Nested Loops

Now consider a different case where the inner loop runs for every iteration of the outer loop:

Outer loop runs times
Inner loop runs times per outer iteration

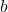
This leads to:

$T(a, b) = a \times b$

In Big-O notation:

$T(a, b) = O(a \times b)$

So, use addition when operations are sequential and multiplication when operations are nested.

2. Logarithmic Time Complexity: Binary Search

Let’s understand logarithmic complexity using the binary search algorithm.

Binary Search Overview

Given a sorted array of size , binary search follows these steps:

Check the middle element.
If target is smaller, search left half.
If target is larger, search right half.
Repeat until the element is found or subarray size becomes 1.

Each step halves the number of elements to process.

Complexity Analysis

Suppose the array size is .

Each iteration reduces the problem size by half:

Iteration 1: $n = 16$
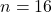
Iteration 2: $n = 8$
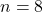
Iteration 3: $n = 4$
Iteration 4: $n = 2$
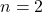
Iteration 5: $n = 1$

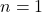
So, number of operations needed is approximately:

$k = \log_2 n + 1$

Hence,

$T(n) = O(\log n)$

This logarithmic time complexity arises in many algorithms that divide the problem in half each time.

3. Impact of Strings on Complexity

3.1 Comparing Strings

When comparing strings like:

if (s1 > s2)

The algorithm compares each character one-by-one until a difference is found. In the worst case, all characters are compared.

If is the length of the string, then:

$T(n) = O(n)$

3.2 String Concatenation

In many languages (Java, JavaScript, C#), strings are immutable. So concatenating strings creates a new string each time:

s3 = s1 + s2

Steps:

Calculate total length
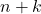
Allocate new array
Copy characters from s1
Copy characters from s2
Create new string

Hence,

$T(n, k) = O(n + k)$

3.3 Substring Operation

When extracting a substring:

s2 = s1.substring(start, end)

Steps:

Calculate new length:
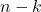
Allocate array of size
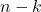
Copy characters
Create new string

Thus:

$T(n, k) = O(n - k)$

And in worst-case (where ), it still simplifies to:

$O(n)$

4. Repeated String Concatenation in Loops

Consider this code:

String s = "";
for (int i = 0; i < n; i++) {
    s = s + "A";
}

Each iteration creates a longer string:

Iteration	String Length	Operation Cost
1	1	1
2	2	2
3	3	3
…	…	…
n	n	n

The total time complexity:

$T(n) = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2}$

Therefore,

$T(n) = O(n^2)$

5. Summary of Key Concepts

Sequential vs Nested Loops

Sequential → $O(a + b)$
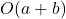
Nested → $O(a \times b)$

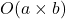
Logarithmic Algorithms

Halving each time → $O(\log n)$