Amortized Analysis

Amortized analysis is a powerful technique used to analyze the time complexity of algorithms, especially when an occasional expensive operation is offset by many cheap ones. Let’s explore this concept step-by-step with a concrete example.

Understanding the Problem

Suppose we have a fully filled array of $n$ elements, and we want to insert one more element. The typical algorithm to do this involves:

Creating a new array of size $n + 1$ .
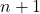Copying 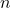$n$ elements from the old array into the new one.
Inserting the new element.

The complexity of copying $n$ elements is $O(n)$ , and inserting a new element is $O(1)$ . Therefore, the total time complexity is:

$T(n) = n + 1 = O(n)$

Can We Improve It?

The question arises: Can we design a data structure where inserting elements is always $O(1)$ and retrieving any element is also $O(1)$ ?

The answer is yes, and one such structure is Java’s ArrayList. It offers:

Infinite logical capacity.
Element insertion complexity: 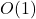$O(1)$ (amortized).
Single element retrieval complexity: $O(1)$ .

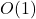But how is this achieved?

Internal Working of ArrayList

Internally, ArrayList uses an array. When the internal array is full, it creates a new array of twice the size. Then:

Copies all existing elements into the new array.
Inserts the new element.

Example: Inserting 7 into [5, 3, 1, 9] triggers resizing:

New array is created with size 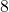$8$ (if current size is $4$ ).
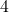Old elements are copied: 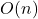$O(n)$ time.
New element is inserted: $O(1)$ .

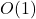We call such insertions boundary insertions—those that trigger array resizing.

So:

Non-boundary insertions: $O(1)$
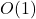
Boundary insertions: $T(n) = n + 1 = O(n)$

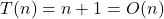
Need for Amortized Analysis

Using worst-case time complexity ( $O(n)$ ) for each insertion would be too pessimistic because most insertions are cheap. Instead, we use amortized analysis, which averages the cost over a sequence of operations.

Amortized analysis answers:

What is the average cost of each operation in a sequence of $n$ operations?

Aggregation Method (Most Common Approach)

Steps:

Compute total time for a sequence of 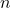$n$ insertions (including cheap and expensive ones).
Use the formula:

$\text{Amortized Cost} = \frac{\text{Total Cost of } n \text{ insertions}}{n}$

Let’s understand this with an example: inserting elements from $0$ to $16$ into an initially empty ArrayList.

Visualizing Resizing and Copy Operations

Let’s build a table:

Insertion Index	Boundary Element?	Copy Operations
0	Yes	0
1	Yes	$2^0$ = 1
2	Yes	$2^1$ = 2
4	Yes	$2^2$ = 4
8	Yes	$2^3$ = 8
16	Yes	$2^4$ = 16

Each time the size reaches a power of 2, a resize (boundary insertion) is triggered. So:

Total copies due to resizing: $2^0 + 2^1 + 2^2 + 2^3 + 2^4 = \sum_{i=0}^{4} 2^i$
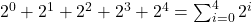
Number of insertions: 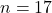$n = 17$ (from 0 to 16)

Using the formula for geometric series:

$\sum_{i=0}^{k} 2^i = 2^{k+1} - 1$

Since $n = 2^k$ , then $k = \log_2 n$ . So total copy operations = $2n - 1 = O(n)$ .

Also, there are $n$ insertions, each with $O(1)$ insertion cost, which totals to $O(n)$ .

Total Complexity of n Insertions

Total time:

$T(n) = \text{Sum of copy operations} + \text{Sum of insertions} = O(n) + O(n) = O(n)$

Amortized Cost Per Insertion

Using the formula:

$\text{Amortized Cost per Insertion} = \frac{T(n)}{n} = \frac{O(n)}{n} = O(1)$

Summary and Final Notes

Worst-case cost of a single insertion: $O(n)$
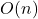
Best-case cost of a single insertion: $O(1)$
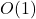
Amortized cost per insertion (over a sequence): $O(1)$

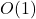
That’s why ArrayList can offer fast average-time insertions, even though some insertions take linear time.