What Is Space Complexity?

As discussed earlier, algorithm complexity includes two main components:

1. Time Complexity – the amount of time needed to complete the algorithm.
2. Space Complexity – the amount of memory required to complete the algorithm.

In this section, we’ll focus on the space complexity, which is usually denoted as the function .

All the rules for evaluating space complexity using Big-O notation are identical to those used for time complexity.

Example 1: Simple Function Call

Let’s consider a simple function:

doubleNum(int x) {
    return x * 2;
}

foo(int n) {
    for (int i = 1; i <= n; i++) {
        doubleNum(i);
    }
}

When calling , here’s what happens:

• The function 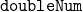is called inside a loop.
• Each call to 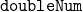creates a stack frame in memory (RAM), which includes local variables and system data.
• As soon as the function completes, its stack frame is removed from memory.

So, at any given moment, only one stack frame is present in memory.

Thus, space complexity is:

Example 2: Recursive Function

Now, let’s analyze the space complexity of a recursive function:

foo(int n) {
    if (n == 1) return;
    foo(n - 1);
}

Let’s execute .

• Calling 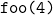creates a stack frame.
• Then is called → another stack frame is added.
• Then 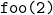, and finally .

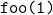So, at one point, we have 4 stack frames in memory.

Therefore, space complexity is:

This happens because recursive calls accumulate on the call stack before returning.

Example 3: Recursive Function with Multiple Calls

Let’s now analyze a recursive function that makes two recursive calls:

foo(int n) {
    if (n == 1) return;
    foo(n - 1);
    foo(n - 1);
}

You might think the entire recursive tree of calls remains in memory—but that’s not true.

Here’s what actually happens:

• The recursive tree is traversed depth-first.
• At most, the memory holds a path from root to leaf, which is the height of the tree.

So, for , the maximum number of active stack frames is 4 (i.e., the height of the tree).

Thus, even though the function makes calls over time, the space complexity remains:

Type of Function	Space Complexity
Non-recursive function
Single-recursive call
Multiple-recursive calls	(due to call stack depth)

Strings and Space Complexity

Now, let’s evaluate how string operations impact space complexity.

String Concatenation

In most languages (e.g., Java, JavaScript), strings are immutable. That means every time you concatenate a string, a new string is created.

So, if you concatenate a string of length with one character, the memory required is:

Example: Loop Concatenation

String s = "";
for (int i = 1; i <= n; i++) {
    s = s + "a";
}

Let’s break it down:

Iteration	New String	Space Used
1	“a”
2	“aa”
3	“aaa”
…	…	…
n	“aaaa…a”

Total space used across all iterations:

Final Summary

Let’s consolidate everything:

• Non-recursive function:
  

Recursive function (single call):

Recursive function (multiple calls):

String concatenation once:

String concatenation inside a loop: