Typical Complexities in Algorithm Analysis

When evaluating the complexity of an algorithm, you’ll frequently encounter a few common patterns. Understanding how to approximate, calculate, and represent them using Big-O notation is a crucial step in analyzing algorithm efficiency.

Let’s break down the most common complexity patterns and how to handle them.

1. Arithmetic Series: $1 + 2 + 3 + \ldots + n$

This is a classic arithmetic series.

The exact sum is:

$1 + 2 + 3 + \ldots + n = \frac{n(n + 1)}{2} = \frac{n^2 + n}{2}$

But in Big-O notation, we drop constants and lower-order terms:

$O(n^2)$

How to Remember It (Visual Intuition)

Suppose you had this sum:

$4 + 3 + 2 + 1 = 10$

You can visualize it as a triangle. This sum is roughly:

$\frac{n^2}{2}$

So in Big-O, it becomes:

$O(n^2)$

Even if you forget the formula, you can remember it grows quadratically because the number of additions grows like a triangle.

2. Geometric Series: 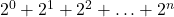$2^0 + 2^1 + 2^2 + \ldots + 2^n$

This is a geometric series with ratio 2.

The exact sum is:

$2^{n+1} - 1$

We approximate this as:

$O(2^n)$

How to Visualize

Let’s take $n = 4$ :

$1 + 2 + 4 + 8 + 16 = 31$

Now imagine each number as circles:

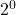$2^0$ = 1 circle
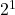$2^1$ = 2 circles
…
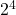$2^4$ = 16 circles

If you stack all these over the last row ( $2^n$ ), it gives an area roughly double of the last row:

$2^{n+1}$

Which, in Big-O, simplifies to:

$O(2^n)$

3. Logarithmic Base Conversion

If you’re dealing with logarithms of different bases, remember this formula:

$\log_A n = \frac{\log_B n}{\log_B A}$

Here:

$A > 1$
$B > 1$
$n > 0$

Since $\log_B A$ is constant, and Big-O ignores constants:

$\log_A n = O(\log n)$
$\log_B n = O(\log n)$

So, in complexity analysis, all logarithms are treated equally.

4. Factorial: 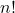$n!$

The factorial function grows very fast. It’s the product of all positive integers up to $n$ :

$n! = 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n$

Special case:

$0! = 1$

Example:

$3! = 1 \cdot 2 \cdot 3 = 6$

Growth Order

Factorial growth: $O(n!)$
This is faster than exponential: $2^n$

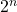
5. Permutations

The total number of permutations of $n$ unique elements is:

$P_n = n!$

Example: For $n = 3$ (elements A, B, C), the permutations are:

Total permutations: $3! = 6$

6. Summary of Typical Complexities

7. Useful Formulas to Remember

Arithmetic sum:

$1 + 2 + 3 + \ldots + n = \frac{n(n + 1)}{2}$

Geometric sum:

$2^0 + 2^1 + \ldots + 2^n = 2^{n+1} - 1$

Logarithmic base change:

$\log_A n = \frac{\log_B n}{\log_B A}$

Factorial:

$n! = 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n$

Permutations:

$P_n = n!$

8. Conclusion

When evaluating time complexities of algorithms:

Use approximations when exact values are hard to remember.
Recognize standard patterns like arithmetic, geometric, and factorial growth.
Apply Big-O notation to express the order of growth.
Ignore constants and lower-order terms, focusing only on the leading term.

These foundational patterns appear repeatedly in sorting, searching, recursion, and combinatorics. Mastering them will greatly improve your skill in analyzing algorithms.

Expression	Complexity
$1 + 2 + 3 + \ldots + n$	$O(n^2)$
$2^0 + 2^1 + 2^2 + \ldots + 2^n$	$O(2^n)$
$\log_A n$ or $\log_B n$	$O(\log n)$
$n!$	$O(n!)$
Permutations $P_n$	$O(n!)$